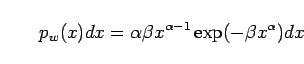Wave and crest height distribution

First, it is assumed unidirectional, stationarity and ergodicity for wave field. The most widely used statistical distribution describing wave height and crest/trough amplitude is the Weibull distribution. As a starting point of this study, it is assumed that the PDF of wave/crest height can be described by the Weibull distribution (Kendall and Stuart, 1963) given by

$$p_{w}(x)dx = \alpha\beta x^{\alpha-1}\exp(-\beta x^\alpha)dx$$ (1)

where $\alpha$ and $\beta$ are coefficients of the Weibull distribution, and $x$ is a random variable such as crest or wave height normalized, for example, by the root-mean-square of the free surface fluctuations, $\eta_{rms}$. For the cases of $\alpha$=2 with $\beta$=1/8 or $\beta$=1/2, Eq.(1) is equivalent to the Rayleigh distribution for wave height or crest/trough amplitude distributions, respectively. In this study, the one parameter Weibull distribution is adopted to simplify the problem. Therefore, the value of $\beta$ is fixed as 1/8 for wave height and 1/2 for crest amplitude distributions, and $\alpha$ is assumed larger than 1. If vertical wave symmetry is assumed, then the wave height $H$ is defined by twice the wave amplitude $A$. For the Rayleigh distribution of wave height, Eq.(1) gives

$$\frac{ \bar{H} }{ \eta_{rms} } = \int_{0}^{\infty} x p_w(x)dx = \sqrt{2\pi}$$ (2)

$$\frac{ H_{rms}^2 }{ \eta_{rms}^2 } = \int_{0}^{\infty} x^2 p_w(x)dx = 8$$ (3)

and for the Rayleigh distribution of wave amplitude, Eq.(1) gives

$$\frac{ \bar{A} }{ \eta_{rms} } = \int_{0}^{\infty} x p_w(x)dx = \sqrt{\frac{\pi}{2}}$$ (4)

$$\frac{ A_{rms}^2 }{ \eta_{rms}^2 } = \int_{0}^{\infty} x^2 p_w(x)dx = 2$$ (5)

where the over-bar indicates the mean value.

For the deck overtopping problem, the wave crest amplitude is the dominant variable compared with either the wave trough amplitude or wave height, although wave period is also important for overtopping. Moreover, the wave nonlinearities enhance vertical asymmetry of waves, and, as a result, the wave crest amplitude is generally larger than its trough amplitude. Therefore, only Eq.(1) for the PDF of wave crest amplitude is used hereafter. This implies that for fixed $\beta$=1/2, $\alpha$ is the only empirical parameter controlling profile of the distribution. The mean and rms value of Eq.(1) with $\beta=1/2$ are given by

$$\frac{ \bar{A} }{ \eta_{rms} } = \frac{ 2^{ \frac{1}{\alpha} } }{ \alpha } \,\Gamma\left( \frac{ 1 }{ \alpha },0 \right)$$ (6)

$$\frac{ A_{rms}^2 }{ \eta_{rms}^2 } = \frac{ 2^{ 1 + \frac{2}{\alpha} } }{ \alpha } \,\Gamma\left( \frac{ 2 }{ \alpha },0 \right)$$ (7)

where $\Gamma$ is the incomplete gamma function defined by

$$\Gamma\left( a,z \right) = \int_{z}^{\infty} t^{a-1} e^{-t} dt$$ (8)

Eq.(6) and (7) with $\alpha$=2 are equivalent to the Rayleigh distribution defined by Eq.(4) and (5).

If the deck is thin compared to the incident wave amplitude, then the influence of the deck on the incident wave profile is negligible. In this case, the PDF of the wave amplitude distribution on the deck can be described by a truncated form of Eq.(1):

$$p_w(A')dA' = \left\{ \begin{array}{l@{\ \ \ }l} \displa... ...dA' & A' \ge z_c' \\ 0 & A' < z_c' \\ \end{array} \right.$$ (9)

where the $'$ indicates a normalized value, and $A'$ and $z'_c$ are the wave amplitude and deck level normalized by the rms value of the surface elevation $\eta_{rms}$ in the absence, or well seaward, of the deck. Eq.(9) gives the exceedance probability of the wave amplitudes on the deck:

$$P_w(A') = \left\{ \begin{array}{l@{\ \ \ }l} \displayst... ... } & A' \ge z_c' \\ 1 & A' < z_c' \\ \end{array} \right.$$ (10)

Figure 3: Illustration of geometrical location of deck and incident wave.

=10cm

The same number of waves in Eq.(9) and Eq.(10) is used in Eq.(1). Therefore, the small amplitude wave which is smaller than $z_c$ is also taken into consideration in in Eq.(9) and Eq.(10). Obviously, the equivalence assumption of $\alpha$ between Eq.(1) and Eq.(9) depends on the thickness of the deck in comparison with the incident wave height and wave nonlinearity. The effect of the structure on the total wave height is minimal, if the deck is thin and has little influence on the incident wave. On the other hand, $\alpha$, is to be determined empirically. Mori (2003) used experimental data to investigate the relationship between $\alpha$ and the kurtosis, $\mu_4$, of the surface elevation for deep-water random waves. The regression curve given by Mori (2003) is

$$\alpha = 3.0\exp(-0.147\mu_4).$$ (11)

For the case of $\mu_4$=3.0, Eq.(11) gives $\alpha \simeq 2.0$, consistent with linear Gaussian theory. The value of $\alpha$ is directly calculated from the experimental data by maximum likelihood method as shown in Table 1. For Case 1 of the present data set, the observed values of $\alpha$ and $\mu_4$ were 1.78 and 3.38, respectively, whereas Eq.(11) gives an estimate of $\alpha$=1.82, a difference of 4%. Therefore, if the value of kurtosis is given, then $\alpha$ is obtainable from the empirical relationship for thin deck level case. However, the estimation of $\alpha$ is beyond of this study, and further understanding of its relationship to other sea-state parameters is abandoned here.

Figure 4: Model/data comparison of PDF of normalized wave crest amplitude with experimental results (solid), Rayleigh wave amplitude distribution (dash) and Weibull wave amplitude distribution (chain) for (a) Case 1 and (b) Case 2.

=11cm

(a) Case 1.

=11cm

(b) Case 2.

Fig.4 compares the measured PDF of normalized wave crest amplitudes with the computed PDFs for the Rayleigh amplitude distribution and the Weibull amplitude distribution, Eq.(1). The kurtosis values of the incident waves were about 3.4 and 3.3, respectively (Table 1). Therefore, the incident wave field was highly nonlinear compared to observations of real ocean waves. This difference may be to due to three dimensional or wind effects not present in the hydraulic model study. Since the values of $\alpha$ were smaller than 2.0, the peak of the Weibull distribution is lower than that of the Rayleigh distribution, and the tail of the Weibull distribution is higher. The Weibull distribution gives an overall better fit to the experimental data compared to the Rayleigh distribution.

Figure 5: Model/data comparison of exceedance probability of normalized wave crest amplitude for (a) Case 1 and (b) Case 2 with Gage 1 ($\circ$), Gage 2 ($\times$), Rayleigh distribution at $z=0$ (dashed), Weibull distribution at $z=0$ (chain), Rayleigh distribution at $z=z_c'$ (solid), Weibull distribution at $z=z_c'$ (dotted).

=11cm

(a) Case 1.

=11cm

(b) Case 2.

Fig.5 compares the exceedance probability of the normalized wave crest amplitude for the experimental results at Gage 1 and 2 with the Rayleigh and Weibull distributions for Case 1 and 2. The exceedance probability of the Weibull distribution is calculated by Eq.(10) and the Rayleigh distribution is calculated by Eq.(10) with $\alpha=2$. The Weibull distribution gives better agreement to the experimental data for the seaward location (Gage 1) for both cases and for the waves on the deck (Gage 2) for the lower deck case (Case 1). For the higher deck case (Case 2), the experimental data is located in between that of the Weibull and Rayleigh distributions on the deck.