

Next: Formulation of PDF of
Up: Mathematical formulations
Previous: Wave and crest height
The overtopping volume, 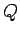 , can be defined as the volume of water
column above the deck level, shown schematically
in Fig.1.
The overtopping volume
, can be defined as the volume of water
column above the deck level, shown schematically
in Fig.1.
The overtopping volume 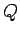 only depends on spatial surface profile, if
the deck is thin compared to the incident wave amplitude.
Therefore, if the spatial wave profile is known, it is possible to
calculate the overtopping volume
only depends on spatial surface profile, if
the deck is thin compared to the incident wave amplitude.
Therefore, if the spatial wave profile is known, it is possible to
calculate the overtopping volume 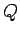 accurately.
However, there is some difficulty to estimate the spatial profile of
random waves.
Thus, the overtopping volume
accurately.
However, there is some difficulty to estimate the spatial profile of
random waves.
Thus, the overtopping volume 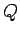 is calculated by the following assumptions and procedure.
First, the profile of the individual wave crest is assumed to be a sinusoidal wave locally.
Then, if the deck level
is calculated by the following assumptions and procedure.
First, the profile of the individual wave crest is assumed to be a sinusoidal wave locally.
Then, if the deck level 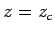 is given and the crest amplitude
is given and the crest amplitude 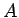 is known, the
volume of water column above deck level,
is known, the
volume of water column above deck level, 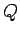 , is simply calculated by
, is simply calculated by
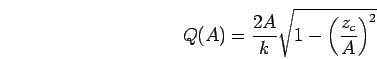 |
(11) |
where 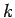 is the local wave number and
is the local wave number and 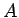 is local amplitude of the wave.
Eq.(11) can be roughly simplified for
is local amplitude of the wave.
Eq.(11) can be roughly simplified for 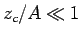 as
as
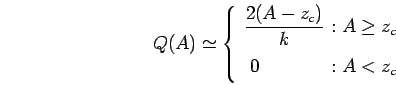 |
(12) |
Fig.2 shows an example of Eq.(11) and (12)
for the cases of 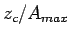 = 0.1 and 0.5.
The transformation of the wave amplitude
= 0.1 and 0.5.
The transformation of the wave amplitude 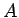 into overtopping volume
into overtopping volume 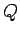 by
the approximate
Eq.(12) becomes worse as the height of the deck level
by
the approximate
Eq.(12) becomes worse as the height of the deck level 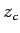 increases.
The overtopping volume
increases.
The overtopping volume 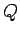 decreases as
decreases as 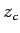 increases as expected.
Obviously, the assumptions of the local sinusoidal
wave crest profile and local wave number are only valid for narrow banded spectra.
The validity of the assumptions will be discussed later in
the context of the experimental results.
increases as expected.
Obviously, the assumptions of the local sinusoidal
wave crest profile and local wave number are only valid for narrow banded spectra.
The validity of the assumptions will be discussed later in
the context of the experimental results.
The overtopping volume 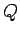 can be normalized by the rms value of surface
elevation
can be normalized by the rms value of surface
elevation 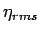 and wavenumber
and wavenumber 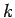 as
as
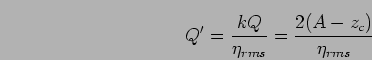 |
(13) |
From Eq.(13), the inverse relationship between 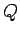 and
and 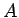 is given by
is given by
 |
(14) |
The upper script 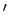 for
for 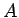 ,
, 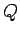 and
and 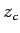 will be dropped for
simplification hereafter.
All equations and variables are normalized by
will be dropped for
simplification hereafter.
All equations and variables are normalized by 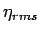 following section.
following section.


Next: Formulation of PDF of
Up: Mathematical formulations
Previous: Wave and crest height
2002-11-26
![]() , can be defined as the volume of water
column above the deck level, shown schematically
in Fig.1.
The overtopping volume
, can be defined as the volume of water
column above the deck level, shown schematically
in Fig.1.
The overtopping volume ![]() only depends on spatial surface profile, if
the deck is thin compared to the incident wave amplitude.
Therefore, if the spatial wave profile is known, it is possible to
calculate the overtopping volume
only depends on spatial surface profile, if
the deck is thin compared to the incident wave amplitude.
Therefore, if the spatial wave profile is known, it is possible to
calculate the overtopping volume ![]() accurately.
However, there is some difficulty to estimate the spatial profile of
random waves.
Thus, the overtopping volume
accurately.
However, there is some difficulty to estimate the spatial profile of
random waves.
Thus, the overtopping volume ![]() is calculated by the following assumptions and procedure.
First, the profile of the individual wave crest is assumed to be a sinusoidal wave locally.
Then, if the deck level
is calculated by the following assumptions and procedure.
First, the profile of the individual wave crest is assumed to be a sinusoidal wave locally.
Then, if the deck level ![]() is given and the crest amplitude
is given and the crest amplitude ![]() is known, the
volume of water column above deck level,
is known, the
volume of water column above deck level, ![]() , is simply calculated by
, is simply calculated by
![]() can be normalized by the rms value of surface
elevation
can be normalized by the rms value of surface
elevation ![]() and wavenumber
and wavenumber ![]() as
as
![\includegraphics[width=12.0cm]{figures/theory_amplitude-volume.eps}](img46.png)