

Next: Acknowledgments
Up: Statistical Modeling of Overtopping
Previous: Model/Data Comparisons and Discussions
Although much attention has been given to the statistical formulations
for extreme crest distribution in the context of the air gap problem
for offshore platforms and for wave overtopping of coastal structures in
shallow water, relatively little work has been done to investigate
the wave overtopping for a fixed deck.
In this paper, equations typically used to describe extreme crest ampitude
distributions were extended to formulate a statistical model which
would describe the exceedance probability for the
normalized volume of water overtopping a fixed deck under
extreme (nonlinear) wave conditions. The model relies on only
a few parameters, notably the deck height, the root-mean-square
of the incident waves, and a Weibull parameter representing
the nonlinearity of the wave condition.
Several assumptions were used to simplify the formulation. The
most significant of these are the assumption of narrow banded
spectra, locally sinusoidal wave profile, thin deck, and low deck.
To check these assumptions and to validate the statistical model,
comparisons were made with small-scale laboratory measurements in
a narrow (two-dimensional) wave flume. Typical JONSWAP wave spectra were
used with over 3000 incident waves for each case. Measurements included
the free surface variations seaward of the deck and the overtopping
rate
on the leading edge of the deck.
The overtopping volume was normalized by 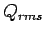 ,
, 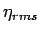 and
and 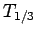 from the total wave field measured seaward of the deck and were similar for both cases.
The comparisons of the statistical model and measurements showed that
from the total wave field measured seaward of the deck and were similar for both cases.
The comparisons of the statistical model and measurements showed that
- The Weibull distribution gives a better agreement of the
exceedance probability for crest amplitudes seaward of the
deck compared to the Rayleigh theory, and that the Weibull
distribution gives a better agreement on the deck for lower
deck heights
(Fig. 10).
- The modified Rayleigh overtopping distribution shows fair agreement
with the experimental data for small values of
 ,
and the modified Weibull overtopping distribution
gives excellent agreement for large values of
,
and the modified Weibull overtopping distribution
gives excellent agreement for large values of  (Fig. 13).
(Fig. 13).
Additional quantitative verification of the statistical model and extension of the theory
to overtopping rate will be studied in the future.
Upon further refinement, the model be useful to predict and understand the
overtopping on the
deck for engineering use.


Next: Acknowledgments
Up: Statistical Modeling of Overtopping
Previous: Model/Data Comparisons and Discussions
2002-11-26
![]() ,
, ![]() and
and ![]() from the total wave field measured seaward of the deck and were similar for both cases.
The comparisons of the statistical model and measurements showed that
from the total wave field measured seaward of the deck and were similar for both cases.
The comparisons of the statistical model and measurements showed that