

Next: Conclusion
Up: Numerical Results and Discussions
Previous: Surface wave profile and
The high-order nonlinearities increase
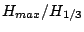 , kurtosis and
, kurtosis and  .
Another significant aspect of the high-order nonlinear effects is an exceedance probability of wave heights.
Figure 9 shows comparison of exceedance probabilities of wave heights among the high-order nonlinear solution (filled circle), second-order one (filled triangle) and the Rayleigh distribution (dashed line) for
.
Another significant aspect of the high-order nonlinear effects is an exceedance probability of wave heights.
Figure 9 shows comparison of exceedance probabilities of wave heights among the high-order nonlinear solution (filled circle), second-order one (filled triangle) and the Rayleigh distribution (dashed line) for 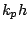 =
=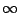 and 1.36.
The exceedance probabilities of wave heights of the second-order solution are independent of the water depth and are slightly below the Rayleigh distribution.
On the other hand, the exceedance probabilities of wave heights of the high-order solution exceed the Rayleigh distribution in deep-water and are the same to the second-order solution in
and 1.36.
The exceedance probabilities of wave heights of the second-order solution are independent of the water depth and are slightly below the Rayleigh distribution.
On the other hand, the exceedance probabilities of wave heights of the high-order solution exceed the Rayleigh distribution in deep-water and are the same to the second-order solution in 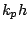 =1.36.
This tendency of the exceedance probability of wave heights is the same as kurtosis.
The result of numerical simulation clearly shows that the wave height distribution is not constant but varies as a function kurtosis.
The authors investigated the nonlinear wave height distribution as a function of kurtosis in references (Mori and Yasuda, 1996; Mori and Yasuda, 2000; Mori and Yasuda, 2002).
=1.36.
This tendency of the exceedance probability of wave heights is the same as kurtosis.
The result of numerical simulation clearly shows that the wave height distribution is not constant but varies as a function kurtosis.
The authors investigated the nonlinear wave height distribution as a function of kurtosis in references (Mori and Yasuda, 1996; Mori and Yasuda, 2000; Mori and Yasuda, 2002).
2005-11-21